Метод аналогии при изучении темы  «Многогранники».

Для познания мира одного эмпирического метода одних наблюдений и даже их анализа недостаточно, существуют ситуации, когда опыт не в состоянии дать ответ на возникающие у человека вопросы, и приходится прибегать к умозрительным конструкциям, к цепочке доказательств, к логике, к дедукции и индукции.     Изучение темы «Многогранники» позволяет расширить и систематизировать сведения о пространственных фигурах – многогранниках.

Неоценимая роль темы «Многогранники» состоит в том, чтобы показать обучающимся их разнообразие и многочисленное присутствие в окружающей нас действительности. При изучении тем: «Призма», «Пирамида» и «Правильные  многогранники» обучающиеся получают яркое представление об их применении в различных областях человеческой деятельности. При изучения темы по специальности «Технология машиностроения»: использование оптических свойств стеклянной трехгранной призмы для изменения направления хода луча света; четырехгранная призма на конце цилиндрического вала служит для пере­дачи крутящегося момента на вал; модульный принцип конструирования блоков радиоэлект­ронной аппаратуры. Со­товую конструкцию из шестигранных призм при­меняют в качестве сеток, управляющих электронными потоками в электровакуумных приборах. Применение призматических поверхностей в качестве направляющей прямолинейного движения с одной степенью свободы широко используются в различных видах технологического оборудования, особенно в металлорежущих станках.

На протяжении всего курса математики обучающиеся сталкиваются с различными примерами многогранников и отдельными их свойствами. Например, при изучении параллельности в курсе планиметрии находили примеры на натуральной модели куба, параллелепипеда. В процессе изучения данной темы обучающиеся учатся проводить аналогии между плоскими и пространственными фигурами. Например, можно провести аналогию между треугольником и тетраэдром, прямоугольником и параллелепипедом, различными видами четырехугольников и соответствующих им видам призм.

В ходе анализа теоретического материала по теме «Многогранники»  я пришла к выводу, что при построении методики изучения этой темы должны быть учтены некоторые особенности.

Понятие многоугольника аналогично понятию многогранника. В учебниках этим понятиям не дают определения, т. к.  они сложны по своей структуре и требуют введения других понятий. Аналогия проявляется и в их элементах, и в видах. Таким образом, аналогия — является основным методом изучения темы на первых занятиях. Первое занятие эффективнее провести в форме проблемной лекции, на которой будет введено понятие многогранника и рассмотрены его виды – призма и пирамида (изучение пирамиды можно провести как практическую работу).

Итогом данного занятия может быть опорная схема:

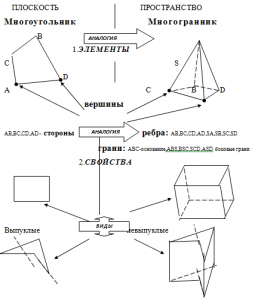
Занятие носит информационный характер, но оно необходимо, т.к. удается систематизировать материал. Более того, лекция построена на методе аналогии, поэтому она несет и познавательный интерес.

При введении нового материала  можно использовать различные формы ЭОР (например, GeoGebra, математический конструктор или мультимедийную доску). Они позволяют не только визуально изучить новую тему, но и попробовать самим с помощью программы построить различные виды фигур, как на плоскости, так и в пространстве, перенести их из плоскости в 3D пространство, используя метод аналогии.

На этом занятии преподаватель показывает обучающимся натуральные модели многогранников, предлагает привести примеры из практики по специальности. Несомненно, обучающиеся имеют представление об этих фигурах, поэтому основная цель изучения данной главы состоит в следующем: систематизировать, расширить, углубить знания по теме.

В теме подробно изучаются фигуры призмы и пирамиды. В определении призмы указано, что боковыми гранями n-угольной призмы являются n параллелограммов. Обучающиеся часто забывают эту фразу определения, произнося его формально. В этом случае необходимо привести контр пример (модель или рисунок), доказав, что упуская это условие, определение теряет смысл.

Виды призм можно вводить также по аналогии с многоугольниками.

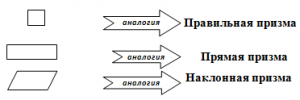
В учебнике фактически доказано существование призмы и пирамиды (построением). При этом очень важно обосновывать каждый шаг построения, используя знания о перпендикулярности и параллельности в пространстве.

Важным умением, которое должно сформироваться у обучающихся, — является построение высот в призме.

Для облегчения понимания предлагается провести аналогию с параллелограммом, т. е. напомнить обучающимся возможность построения высоты не только из вершины, но из любой точки прямой, содержащей его сторону, к противоположной стороне.

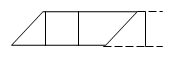
По аналогии, высоту призмы можно проводить из любой точки плоскости верхнего основания к плоскости, содержащей нижнее основание.

Список литературы:

1. В помощь учителю математики (методические рекомендации по решению стереометрических задач на доказательство и вычисление). – Горький, 1984.
2. Гончаренко, Б.Г. Задачи и вопросы по стереометрии / для устного решения /. Многогранники и тела вращения. – М.: Просвещение, 1964, 96с.
3. Груденов Я. И. Совершенствование методики работы учителя математики Далингер В. А. Об аналогиях в планиметрии и стереометрии // Математика в школе. – 1995. — № 6.
4. Гусев В.А., и др. Методика обучения геометрии. Учеб. пособие для студентов высш. учеб. заведений (В.А.Гусев, и др; Под ред. В.А. Гусева. – М.: Издательский центр «Академия».2010, 368с.
5. Саакян С.М., Бутузов В.Ф. Изучение темы «Многогранники» в курсе 10 класса // Математика в школе. – 2000. – № 2. – С. 19.